Compiler

Compiling Quantum Gates

Most quantum algorithms require only single qubit gates and entangling two qubit gates, which are combined into complex circuits. However, physical implementation of quantum computers can often only realize a limited set of gates reliably. Other gates, that do not belong to this instruction set, have to be approximated by sequences of these gates. The task of the quantum compiler is given an arbitrary gate to find a sequence the approximates it within a small error. The universal set of quantum gates that is used can be found (and changed) in the module instruction_sets.py :

>>> from QuackQuack.compiler.instruction_sets import universal_gates
>>> n = 2                  # compile single qubit gates
>>> G = universal_gates[n] # Hadamard, pi/8-gate and complex conjugates

Solovay-Kitaev Algorithm

The Solovay-Kitaev algorithm [1] can iteratively produce better approximations, but it needs a crude initial approximation to the gate in order to converge. The program QuackQuack/compiler/basic_approximations.py generates basic approximations by simply enumerating all possible combintations of simple gates up to a certain length:

cd QuackQuack/compiler/
python basic_approximations.py 2 12

This will generate a set of basic approximations for 2x2 matrices of up to 12 gates and store them in a database in /tmp/gate_library/basic_approximations/U2x2/ for later use. You can load this basic approximation with the following commands:

>>> from QuackQuack.compiler.basic_approximations import IdentityReduction, BasicApproximation, load_basic_approximation
>>> cache = load_basic_approximation(n)

The loaded object allows to retrieve a basic approximation to some unitary 2x2 matrix U as a sequence of indeces into the set of universal gates G.

>>> from QuackQuack.compiler.NumImporter import *
>>> from QuackQuack.compiler.basic_approximations import seq_to_matrix
>>> from QuackQuack.compiler.Solovay_Kitaev import SU_distance
>>> U = array([[1,0],[0,exp(1j*pi/5)]])
>>> Useq = cache.approximate(U)
>>> Useq                             # 0 -> G[0] ~ Hadamard, 1 -> G[1] ~ Hadamard^+, 2 -> G[2] ~ pi/8, 3 -> G[3] ~pi/8^+
[0, 3, 1, 1, 3, 0, 3, 1, 1, 3, 1, 3]
>>> Uapprox = seq_to_matrix(Useq, G) # multiply gate sequence to get a matrix
>>> print "Error: %s" % SU_distance(U,Uapprox)
Error: 0.111

The method might fail if no gate close enough is found. In this case you should increase the maximal length of the initial sequences and regenerate the basic approximations.

Now we can use the SK-algorithm to find a much better approximation to U. First we need to tell the constructor that the instruction set is in G and that the function cache.approximate provides the basic approximations. We run the SK-algorithm for 5 iterations:

>>> from QuackQuack.compiler.Solovay_Kitaev import Solovay_Kitaev
>>> SK = Solovay_Kitaev(G,cache.approximate)
>>> Useq = SK.approximate(U, 5)
>>> Useq
[1, 2, 2, 0, 3, 1, 3, 1, 2, 1, 3, 1, 3, 1, 3, 0, ...many more indeces...]
>>> Uapprox = seq_to_matrix(Useq, G)
>>> print "Error: %s" % SU_distance(U,Uapprox)
Error: 1.80e-05

U and Uapprox might look quite distinct because they may differ by a global phase and still represent the same gate. SU_distance removes the phase difference before comparison.

[1]	Dawson and Nielsen, “The Solovay-Kitaev algorithm”, http://arxiv.org/abs/quant-ph/0505030v2

Simplification of Gate Sequences

The gate sequences might be unnecessarily long because some combation of gates can be simplified. For instance applying the Hadamard gate (the 0th element of G) twice yields the identity, so the pattern [0,0,x] can be replaced by [x]. The class IdentityReduction finds all replacement rules and applies them to sequences to shorten them.

>>> from QuackQuack.compiler.basic_approximations import IdentityReduction
>>> IdRed = IdentityReduction(G, 3)       # find all patterns of length at most 3
>>> Useq_red = IdRed.replace_identities(Useq)
>>> print len(Useq), len(Useq_red)
36842 33710

The cache with basic approximations already contains an instance, so that the same effect is achieved by:

>>> Useq_red = cache.IdRed.replace_identities(Useq)

Basic Approximations Supplied by a Server

Loading the database with basic approximations and building a search tree can take up a considerable amount of time. Also the database might be too large to fit into memory. For this reason the program approx_server.py allows you to keep the database on a seperate computer with lots of memory and took communicate with that server to get approximations without reloading the database everytime you restart client. First you need to generate a database of basic approximations as above:

cd QuackQuack/compiler/
python basic_approximations.py 2 12

Then start the server (which will listen on “localhost” at port 9999):

python QuackQuack/compiler/approx_server.py 2

You can then (possibly on another computer) get the instruction set and basic approximations with the following code:

>>> from QuackQuack.compiler.approx_server import fetch_approximation, fetch_instruction_set
>>> n = 2
>>> G = fetch_instruction_set(n)
>>> Useq = fetch_approximation(U)
>>> Useq
[1, 3, 0, 0, 3, 0, 3, 0, 0, 3, 0, 3]

Controlled Gates

This implementation of the SK-algorithm can only approximate 2x2 special unitary matrices. To implement many quantum algorithms such as quantum Fourier transform or phase estimation we only require in addition controlled two-qubit gates. If the CNOT gate is available the results in [2] guarantee that we can compile any controlled gate

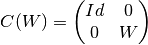
by compiling single qubit gates A,B and C that satisfy

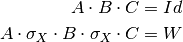
The circuit that implements the controlled W gate then looks like this:

As an example let us compile a controlled pi/10 gate. First start the approximation server:

python QuackQuack/compiler/approx_server.py 2

Define the pi/10 gate:

>>> PI10 = array([[exp(-1j*pi/10),0],[0,exp(1j*pi/10)]])
>>> controlled_PI10 = block_diag(identity(2,dtype=complex), PI10)

Setup the Solovay-Kitaev algorithm for requesting basic approximations from the server:

>>> from QuackQuack.compiler.approx_server import fetch_approximation, fetch_instruction_set, fetch_simplification
>>> G = fetch_instruction_set(2)
>>> SK = Solovay_Kitaev(G, fetch_approximation)
>>> fetch_simplification.dim=2

Now compile the gates A,B and C and compare with the ideal controlled gate:

>>> from QuackQuack.compiler.basic_approximations import seq_to_matrix_controlled
>>> Aseq,Bseq,Cseq = SK.approximate_controlled(PI10, 5, fetch_simplification)
>>> controlled_PI10_approx = seq_to_matrix_controlled(Aseq,Bseq,Cseq, cache.G)
>>> error = SU_distance(controlled_PI10, controlled_PI10_approx)
>>> print "error = %s" % error
error = 3.933e-05

[2]	Adriano Bernco et.al., “Elementary gates in quantum computation” (1995), Lemma 5.1